مدل DDM یا ارزش‌گذاری تنزیل سود سهام چیست؟ آموزش کامل

مقدمه

بسیاری به دنبال پیداکردن ارزش واقعی سهام شرکت‌ها هستند تا بتوانند با مقایسه‌ی ارزش واقعی و قیمت سهام، برای خرید یا فروش آن تصمیم بگیرند. در واقع ارزش‌گذاری کاربردهای متفاوتی دارد که یکی از این کاربردها، تشخیص تفاوت قیمت سهام و ارزش واقعی آن است. درصورتی‌که قیمت یک سهام بالاتر از ارزش واقعی‌اش قرار داشته باشد، فرصت فروش و درصورتی‌که قیمت کمتر از ارزش واقعی تعیین شده باشد، فرصت خرید ایجاد می‌شود. روش‌های متفاوتی برای ارزش‌گذاری وجود دارد که یکی از آن‌ها ارزش‌گذاری مطلق است. این روش نیز خود شامل چند مدل است که یکی از آن‌ها مدل تنزیل سود سهام (Dividend Discount Model (DDM)) است. در این مقاله به بررسی مدل ارزش‌گذاری یا ارزشیابی تنزیل سود سهام خواهیم پرداخت.

مقدمه‌ای بر مدل DDM

این روش یکی از زیرمجموعه‌های مدل ارزشگذاری ارزش فعلی جریان نقدی (Discounted Cash Flow (DCF)) است. در این حالت ارزش فعلی برابر با جریان‌های نقدی آتی خواهد بود؛ برای اینکه بتوانیم به محاسبه‌ی این روش بپردازیم، لازم است جریان نقدی موردنظر خود را انتخاب کنیم. در حقیقت سه نوع جریان نقدی وجود دارد که با استفاده از آن‌ها می‌توانیم ارزش فعلی را محاسبه کنیم. ما در این مقاله سعی داریم جریان نقدی حاصل از سودهای پرداختی در آینده را مورد بررسی قرار دهیم که به آن مدل ارزشگذاری تنزیل سود سهام یا DDM گفته می‌شود.

تعریف مدل ارزش‌گذاری تنزیل سود سهام مدل DDM

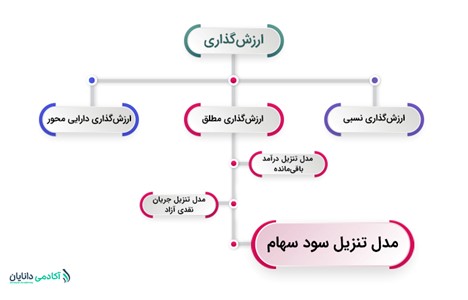
مدل تنزیل سود سهام یکی از روش‌های ارزش‌گذاری مطلق است؛ مدل‌های ارزش‌گذاری مطلق که از آن‌ها به‌عنوان ارزش فعلی نیز یاد می‌شود بر اساس جریان‌های نقدی که در آینده ایجاد خواهد شد، ارزش فعلی یک سهم یا شرکت را تخمین می‌زنند. در واقع این مدل‌ها از یک اصل اساسی علم اقتصاد پیروی می‌کنند که بیان می‌کند افراد مصرف را به تعویق می‌اندازند (سرمایه‌گذاری می‌کنند) تا بتوانند در آینده از منافع این سرمایه‌گذاری بهره‌مند شوند.

شرکت‌ها برای کسب سود، به تولید کالا و ارائه‌ی خدمات می‌پردازند. طی این فعالیت‌ها، جریان نقدی ایجاد می‌شود که سود واحد تجاری را مشخص می‌کند و در نهایت سود حاصل در قیمت سهام منعکس می‌شود. همچنین شرکت‌ها این سودی را که از کسب‌وکارشان ایجاد شده است، بر اساس تعداد سهام، بین سهام‌داران خود تقسیم می‌کنند. یکی از ساده‌ترین مدل‌های ارزش‌گذاری مطلق، مدل تنزیل سود سهام تقسیمی است که یک روش کمی برای محاسبه‌ی ارزش منصفانه‌ی یک سهام، بدون توجه به شرایط حاکم بر بازار است.

در مدل تنزیل سود سهام، ارزش فعلی مجموع سود پرداختی شرکت در آینده را محاسبه می‌کنیم. بر مبنای این مدل به‌منظور محاسبه‌ی ارزش سهام، سودهای نقدی آتی تنزیل و به زمان حال آورده می‌شوند. در واقع ارزش سهام برابر با جمع سودهای نقدی تنزیل شده آتی در نظر گرفته می‌شود. اگر ارزش به‌دست‌آمده از این روش بالاتر از قیمت معاملات فعلی سهام باشد، به این معنی است که سهام کمتر از ارزش واقعی‌اش قیمت‌گذاری شده است و واجد شرایط خرید است و درصورتی‌که مقدار به‌دست‌آمده از قیمت سهام کمتر باشد، به این معنی است که سهام بیشتر از ارزش واقعی‌اش قیمت‌گذاری شده است و موقعیت فروش ایجاد گردیده است.

مروری بر ارزش زمانی پول و ارتباط آن با ارزش‌گذاری

همان‌طور که می‌دانید ارزش پول به‌مرورزمان کاهش پیدا می‌کند. به‌عنوان‌مثال اگر شما در یک بانک برنده‌ی یک جایزه‌ی صد میلیون‌تومانی شوید، ترجیح می‌دهید همین‌الان این جایزه را دریافت کنید یا یک سال دیگر؟ پاسخ مشخص است؛ اغلب افراد ترجیح می‌دهند همین‌الان جایزه را دریافت کنند تا بتوانند با سرمایه‌گذاری این پول در محلی دیگر، مقدار آن را افزایش دهند. به‌عنوان‌مثال اگر نرخ بهره سالیانه بانکی ۵ درصد باشد، با قراردادن این مقدار پول در بانک می‌توان بعد از یک سال ۱۰۵ میلیون تومان دریافت کرد. در نتیجه دریافت آنی پول تصمیم عاقلانه‌تری خواهد بود. برای اینکه بتوانیم باتوجه‌به نرخ بهره، ارزش فعلی یا ارزش آینده‌ی یک مقدار پول را تخمین بزنیم از فرمول‌های زیر استفاده می‌کنیم:

ارزش آینده = ارزش فعلی (۱+ نرخ بهره)

 به همین ترتیب ارزش فعلی برابر خواهد بود با:

ارزش فعلی = ارزش آینده / (۱+ نرخ بهره)

به‌این‌ترتیب درصورتی‌که دو پارامتر از ۳ پارامتر بالا را بدانیم می‌توانیم پارامتر سوم را محاسبه کنیم. مدل تنزیل سود سهام، از این اصل استفاده می‌کند تا ارزش فعلی مجموع تمام سودهایی که در آینده پرداخت خواهد شد را محاسبه کند.

نرخ تنزیل یا نرخ بهره (discount rate)

سهام‌داران با سرمایه‌گذاری در سهام متحمل ریسکی می‌شوند که در ازای آن خواستار بازدهی هستند تا ترغیب شوند این مقدار ریسک را بپذیرند. هرچه ریسک بالاتر باشد، انتظار ما از بازدهی نیز بالاتر خواهد بود و بالعکس. همچنین باتوجه‌به اینکه هزینه‌ها و درآمدهای مربوط به یک طرح در زمان‌های متفاوتی محقق می‌شوند، خواه‌ناخواه نوعی اختلاف زمانی بین هزینه‌ها و درآمدها به وجود می‌آید که باعث می‌شود ارزش واقعی هر واحد پول در سال‌های متفاوت با هم اختلاف داشته باشد.

برای حل این مسائل نرخی تعیین می‌شود تحت عنوان نرخ تنزیل که کمک می‌کند هزینه‌ها و درآمدها بر مبنای یک سال مشخص محاسبه شوند تا قابل قیاس با یکدیگر باشند. همچنین این نرخ، میزان ریسک‌پذیری سرمایه‌گذار را نیز مشخص می‌کند. نرخ تنزیل با نام‌های دیگری چون نرخ بازده یا نرخ تخفیف نیز شناخته می‌شود و در زبان انگلیسی نیز تحت عنوان discount rate  نام‌گذاری شده است. این نرخ با استفاده از مدل CAPM یا مدل رشد سود تقسیمی قابل محاسبه است.

معرفی انواع مدل‌های DDM

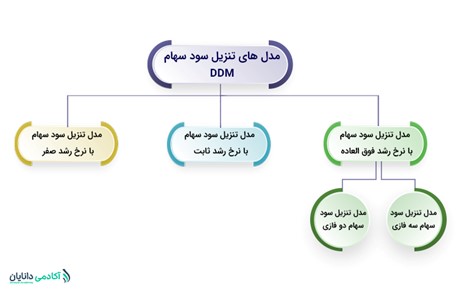مدل تنزیل سود سهام خود شامل ۳ مدل متفاوت است که تفاوت آن‌ها در نرخ رشد سود است. درصورتی‌که سود پرداختی یک شرکت همیشه ثابت باشد، نرخ رشد برابر با صفر خواهد بود. اگر سود پرداختی همواره به مقدار ثابتی افزایش پیدا کند، نرخ رشد مقدار ثابت غیر صفر خواهد داشت و درصورتی‌که افزایش سود پرداختی با نرخ ثابتی صورت نگیرد، نرخ رشد فوق‌العاده خواهیم داشت. در مدل ارزشیابی سهام با فرض رشد در سال‌های آتی، فرض بر این است که کمتر شرکتی وجود دارد که سود هر سهم آن برای همیشه ثابت باشد زیرا اکثر شرکت‌ها به دلیل توسعه‌ی امکانات تولیدی و یا افزایش قیمت محصولات، دارای نرخ رشد مثبت هستند.

 به طور خلاصه ۳ مدل تنزیل سود سهام عبارت‌اند از:

•  بدون رشد
•  سهام با رشد ثابت
•  با رشد فوق‌العاده

فرمول محاسبه‌ی مدل DDM

محاسبه‌ی مدل DDM با درنظر گرفتن نرخ رشد صفر

برای محاسبه‌ی ارزش واقعی یک سهم با استفاده از مدل تنزیل سود سهام (DDM)، می‌توانیم از فرمول محاسبه‌ی ارزش فعلی استفاده کنیم. به‌این‌ترتیب که مجموع ارزش فعلی همه‌ی سودهایی که در آینده تقسیم خواهند شد را با استفاده از این مدل محاسبه می‌کنیم و برابر با ارزش واقعی در نظر می‌گیریم.

D : سود مورد انتظار برای هر سهم

 r: نرخ تنزیل

به همین ترتیب فرمول دیگری نیز وجود دارد که عبارت است از:

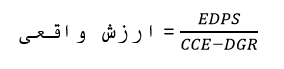
EDPS : سود مورد انتظار برای هر سهم

CCE : هزینه حقوق صاحبان سهام

DGR : نرخ رشد سود سهام

محاسبه‌ی مدل DDM با درنظر گرفتن نرخ رشد

متغیرهایی که در این فرمول محاسبه می‌شوند طبق مفروضات خاصی در نظر گرفته می‌شوند. به همین دلیل باتوجه‌به مفروضات و پیش‌بینی‌هایی مورد انتظار هر سرمایه‌گذار، ممکن است نتایج متفاوتی داشته باشیم. علاوه بر این ازآنجایی‌که سود سهام و نرخ رشد آن، ورودی‌های کلیدی این فرمول هستند، اعتقاد بر این است که مدل تنزیل سود سهام فقط برای شرکت‌هایی که سود سهام عادی پرداخت می‌کنند قابل‌اجرا است. اگرچه برای شرکت‌هایی که سود سهام پرداخت نمی‌کنند نیز می‌توان با درنظرگرفتن پیش‌فرض‌هایی درباره اینکه اگر سود پرداخت می‌کردند، مقدار آن چقدر بود، از این مدل استفاده کرد.

ساده‌ترین مدل تنزیل سود سهام، مدلی است که نرخ رشد را صفر در نظر می‌گیرد. در این صورت ارزش سهام از همان روش گفته شده یعنی مجموع ارزش فعلی سودهای پرداختی در آینده، به دست می‌آید. اما درصورتی‌که نرخ رشد مقداری غیر صفر داشته باشد، از مدل گوردون استفاده می‌کنیم. این مدل که در واقعیت نیز بیشتر رخ می‌دهد بر این اصل استوار است که سود تقسیمی با یک نرخ رشد ثابت هرسال رشد خواهد کرد که به آن مدل رشد پایدار گفته می‌شود. فرمولی که برای محاسبه در این مدل مورداستفاده قرار می‌گیرد عبارت است از:

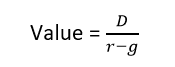
D : سود مورد انتظار

r  : نرخ تنزیل

g : نرخ رشد

محاسبه‌ی مدل DDM با درنظر گرفتن نرخ رشد غیر ثابت

نوع سوم مدل DDM نیز ارتقا یافته‌ی مدل دوم آن است. به این صورت که نرخ رشد آن ثابت در نظر گرفته نمی‌شود. نرخ رشد این مدل تحت عنوان نرخ رشد فوق‌العاده نیز شناخته می‌شود. این مدل ممکن است رشد را به دو یا سه‌فاز تقسیم کند. مرحله اول یک فاز اولیه سریع خواهد بود، سپس یک فاز انتقالی کندتر و در نهایت با نرخ پایین‌تری برای دوره بی‌نهایت به پایان می‌رسد.

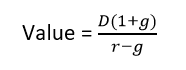
مزایای مدل DDM یا ارزش‌گذاری تنزیل سود سهام

در همه‌ی مدل‌ها و رویکردهای ارزش‌گذاری محدودیت‌هایی وجود دارد، مدل تنزیل سود سهام نیز از این قاعده مستثنی نیست ولی از مزایای این مدل می‌توان درنظرگرفتن نرخ رشدهای متفاوت را عنوان کرد. همچنین نتایج حاصل از یک پژوهش نشان می‌دهد که اختلاف بین قیمت برآوردی سهام با استفاده از مدل سود تقسیم‌شده‌ی تنزیلی و قیمت واقعی سهام، کمتر از سایر مدل‌هاست و قیمت‌های برآوردی با استفاده از این مدل، تقریب نزدیک‌تری به قیمت‌های واقعی سهام ارائه می‌کند.

بیت‌کوین چیست؟

محدودیت‌های روش ارزشیابی تنزیل سود سهام DDM

• مدل DDM  یک روش کمی برای تعیین ارزش ذاتی یک سهم است اما به دلیلی مفروضات و پیش‌بینی‌های زیادی که دارد ممکن است بهترین راه برای پایه‌گذاری تصمیمات سرمایه‌گذاری نباشد.
• برای اینکه بتوانیم از مدل تنزیل سود سهام استفاده کنیم معمولاً لازم است که شرکت موردنظر سودده باشد و سود نقدی پرداخت کند. همچنین تقسیم سود متناسب با سودآوری شرکت باشد و سرمایه‌گذاران یا سهام‌داران عمده نتوانند سیاست تقسیم سود شرکت را تغییر دهند.
• علاوه بر این، مدل گوردون که در آن نرخ رشد مقدار ثابت غیر صفر را در نظر می‌گیریم دارای محدودیت‌هایی است که در ادامه به بیان آن‌ها می‌پردازیم. در حقیقت فرض اول این مدل مبنی بر ثابت بودن نرخ رشد، صرفاً می‌تواند برای شرکت‌های بالغی که سابقه‌ی پرداخت سود منظم دارند صادق باشد. به همین دلیل این مدل تنها برای این شرکت‌ها کاربرد دارد و برای شرکت‌هایی که نرخ رشدشان ثابت نیست تنها در صورتی قابل‌استفاده است که فرضیات دیگری نیز به آن اضافه کنیم.
• علاوه بر این درصورتی‌که نرخ تنزیل از نرخ رشد کمتر باشد، استفاده از این مدل امکان‌پذیر نخواهد بود. این حالت زمانی رخ می‌دهد که یک شرکت متحمل زیان شده باشد اما به پرداخت سود خود مبادرت ورزد.

کاربرد مدل DDM یا ارزش‌گذاری تنزیل سود سهام در سرمایه‌گذاری

همه‌ی مدل‌های ارزشگذاری DDM به ما این امکان را می‌دهند که بدون توجه به شرایط حال حاضر بازار، ارزش‌گذاری را انجام دهیم. همچنین با استفاده از این مدل‌ها می‌توانیم به مقایسه‌ی بین شرکت‌ها بپردازیم. علاوه بر این، همان‌طور که قبلاً نیز گفتیم، با استفاده از این روش می‌توانیم فرصت فروش یا خرید یک سهم را تشخیص دهیم. درصورتی‌که سهم با قیمتی کمتر از ارزش واقعی‌اش معامله شود، فرصت خرید ایجاد می‌شود و درصورتی‌که با قیمتی بالاتر از ارزش واقعی‌اش معامله شود، موقعیت فروش به وجود می‌آید. به‌طورکلی در موارد زیر می‌توان از مدل ارزشگذاری تنزیل سود سهام DDM  استفاده کرد:

• برای شرکت‌هایی که مدت قابل‌توجهی سود تقسیم کرده‌اند و در حال حاضر نیز سود تقسیم می‌کنند. (اما برای شرکت‌هایی که سود تقسیم نمی‌کنند، بهتر است از مدل‌های جریان نقدی آزاد و یا درآمد باقی‌مانده استفاده شود)
• برای ارزش‌گذاری دارایی‌ها در بلندمدت از این مدل استفاده می‌شود.
• برای ارزش‌گذاری شرکت‌هایی که سهام‌داران آن‌ها نمی‌توانند بر سیاست تقسیم سود اثر بگذارند.

جمع‌بندی مدل DDM

روش‌های متفاوتی برای ارزش‌گذاری سهام شرکت‌ها وجود دارد که یکی از آن‌ها روش ارزش‌گذاری تنزیل سود سهام است. در این روش سودهای نقدی آتی تنزیل و به زمان حال می‌آید. در واقع ارزش سهام برابر با جمع سودهای نقدی تنزیل شده آتی را در نظر می‌گیریم. درصورتی‌که نرخ رشد صفر باشد، فرض بر این است که شرکت فاقد رشد است و در شرکت‌هایی که نرخ رشد عددی مخالف صفر قرار دارد، فرض بر این است که شرکت به دلیل توسعه‌ی امکانات تولیدی و افزایش قیمت محصولات، دارای نرخ رشد مثبت در سودهای آتی هستند. در آکادمی دانایان و این مقاله به بررسی کاربرد و محدودیت‌های این مدل پرداختیم و مدل‌های مختلف آن را به طور خلاصه توضیح دادیم.